Resumen: En este artículo se presenta la cámara oscura como un recurso didáctico aplicado en el área de matemáticas. En particular, se verá su uso para poder evaluar la competencia relativa a la utilización del razonamiento matemático en entornos no matemáticos a partir del conocimiento de la trigonometría, en consonancia al currículo correspondiente del cuarto curso de la Educación Secundaria Obligatoria en la Comunidad Autónoma de Cataluña.
Abstract: This paper presents the camera obscura as a didactic resource applied in mathematics. Its use will be seen to be able to evaluate the competence related to the use of mathematical reasoning in non-mathematical environments starting from knowledge of trigonometry, as specified on the corresponding curriculum of the 4th year of Secondary Education in the Autonomous Community of Catalonia.
Palabras clave: Cámara oscura; Matemáticas; Trigonometría; Educación Secundaria Obligatoria.
Keywords: Camera obscura; Mathematics; Trigonometry; Secondary Education.
LA CÁMARA OSCURA COMO RECURSO DIDÁCTICO EN MATEMÁTICAS
La cámara oscura como recurso didáctico en #Matemáticas. #CEdRevistaDigitalDocente Compartir en XÍndice de contenidos
La cámara oscura
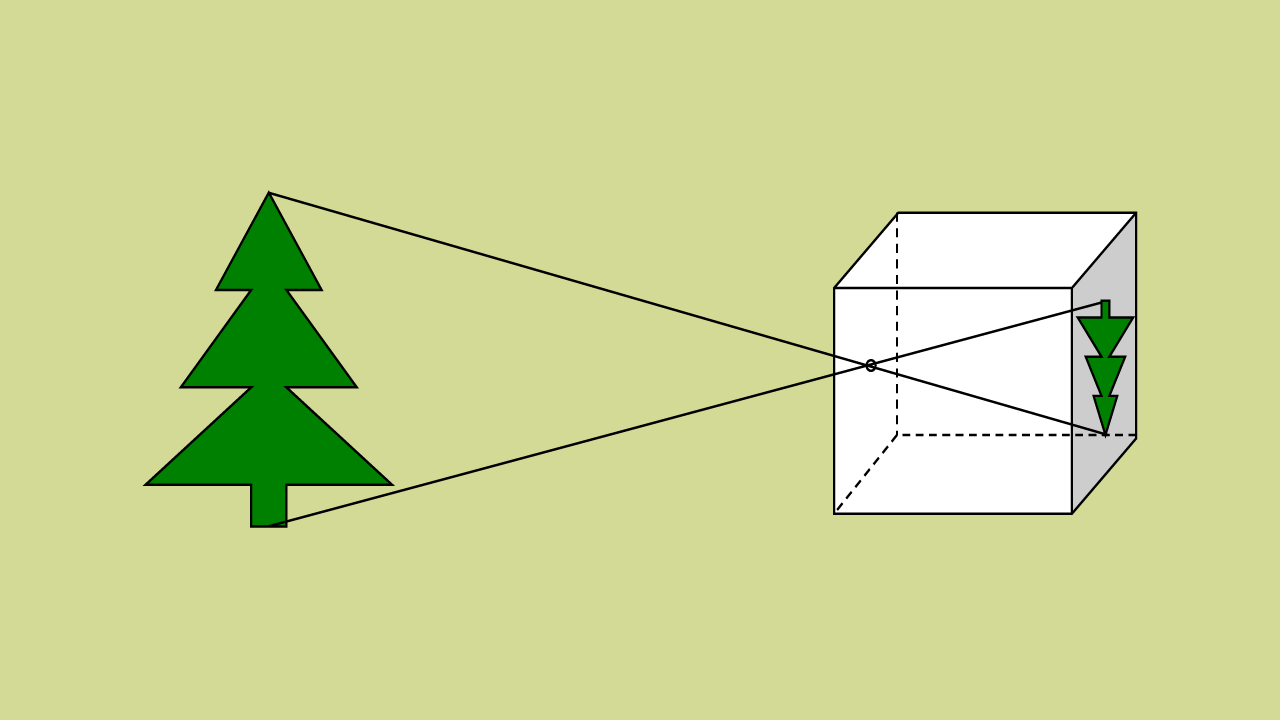
Una cámara oscura es un aparato que puede tener las dimensiones de una cajita o de un habitáculo, pero en todo caso su funcionamiento es siempre el mismo. Se parte de una oscuridad total dentro de la cámara, en la que entra la luz por un único pequeño orificio. La luz muestra la imagen de lo que ocurre en el exterior de la cámara en la pared opuesta en la que está el orificio, que llamaremos pantalla. Supondremos, en este artículo, que el orificio está en el punto central de la cara en que se sitúa.
Fig. 1. Funcionamiento esquemático de una cámara oscura
La relación entre la imagen original y la proyectada es de simetría central y semejanza. Esta cámara oscura se puede mejorar añadiendo lentes en el orificio y también espejos para que la imagen no quede invertida y la relación sea de simple homotecia. La primera opción, de las lentes, solo se mencionará en este artículo. La segunda, relativa a los espejos, escapa a su objetivo.
Una de las utilidades que ofrece la cámara oscura es en el arte, como ayuda al dibujo (se puede adivinar que viene a ser un precursor de la cámara fotográfica). La simetría axial seguida de homotecia favorece una alta precisión tanto en la imagen en sí como en su profundidad cuando se quieren reflejar situaciones reales. Esta ventaja tiene el inconveniente de que en situaciones de poca luz, el artilugio no es operativo.
El descubrimiento de este aparato junto con su simplicidad (entiéndase los modelos más sencillos), así como las conexiones que tiene con diversas materias y las matemáticas que subyacen en él, convierten a la cámara oscura en una candidata óptima para ser usada como recurso didáctico.
Pese a que este artículo toma de referencia la normativa estatal y catalana, es aplicable a cualquier comunidad autónoma, ya que por un lado, como se verá, se incluye en la competencia matemática definida por el Ministerio de Educación y Formación Profesional y, por el otro, las conexiones entre diferentes materias, así como la búsqueda de las matemáticas existentes en entornos no matemáticos, encajan en las propuestas educativas de todos los territorios.
Revisión de propuestas
Si bien es cierto que existen trabajos de propuesta didáctica de la cámara oscura (Criado y otros, 2006; Muñoz-Franco, 2017), el enfoque que presentan es para un uso en las aulas de Educación Primaria, en clase de ciencia, como un estudio de la luz, pero, evidentemente, sin dar ningún enfoque matemático. Es por este motivo que el presente artículo no se puede considerar ampliación o complemento de ninguno anterior, ya que los tratamientos son profundamente dispares.
Propuesta didáctica para 4º de la ESO
En este artículo se propone, por un lado, el conocimiento teórico-práctico de una cámara oscura sin lentes y por el otro, el descubrimiento y tratamiento de la geometría subyacente. La propuesta incluye, como se puede intuir, una colaboración con el departamento de Tecnología para el diseño y construcción de una cámara oscura sencilla. Se hace aconsejable el trabajo en grupos para optimizar el número de aparatos construidos (no es necesario que cada alumno tenga uno) y para el posterior trabajo en el aula de Matemáticas.
Como se ha dicho, hay planteamientos previos del trabajo con cámara oscura para Educación Primara. Este hecho implica, pues, que se puede trabajar la cámara oscura en cualquier etapa de la ESO. Ahora bien, la inclusión de la trigonometría, y la posible ampliación, si se da el caso, al trabajo con lentes (pese a que en si no es objeto del presente artículo), hace que la ubicación que se considera apropiada es la de 4º.
Por una banda, estamos inmersos en el área “El espacio y la forma”, dentro de la competencia matemática, tal y como se describe en la Orden ECD/65/2015, de 21 de enero, por la que se describen las relaciones entre las competencias, los contenidos y los criterios de evaluación de la educación primaria, la educación secundaria obligatoria y el bachillerato.
Por la otra, en el Decreto de la Generalitat de Cataluña 187/2015, de 25 de agosto, de ordenación de las enseñanzas de la educación secundaria obligatoria, se establecen unos Contenidos Clave cuyo encaje es perfecto:
- Sentido espacial y representación de figuras tridimensionales
- Figuras geométricas, características, propiedades y procesos de construcción
- Relaciones y transformaciones geométricas
- Magnitudes y medidas
- Relaciones métricas y cálculo de medidas en figuras.
Esto hace que todas las competencias básicas del ámbito matemático, definidas en el mismo Decreto, lleguen a ser tratadas. Sin embargo, como ya se ha dicho, la competencia que más peso tendrá en esta actividad será la de la utilización del razonamiento matemático en entornos no matemáticos.
Fases de la propuesta
Para el desarrollo de esta propuesta se tendrán que distinguir tres grandes fases, la primera de las cuales es la explicación teórica de la cámara oscura y su funcionamiento, así como algunas herramientas matemáticas; la segunda, en coordinación con el Departamento de Tecnología, el diseño y construcción de alguna de ellas, y la tercera su utilización.
En relación a las dos primeras partes, este artículo no pretende profundizar en ellas pero sí es necesario aquí hacer un inciso en la oportunidad que las nuevas tecnologías aportan para la segunda. La combinación de herramientas clásicas con las más modernas (impresoras 3D por ejemplo), pueden favorecer, en Tecnología, ponderar las ventajas e inconvenientes del uso de diferentes tipos de elaboración, así como las calidades de los resultados.
Siguiendo con la construcción, partiremos del hecho de que trabajaremos con cámaras relativamente pequeñas, de tal manera que no serán habitáculos en los que el alumnado se pueda introducir. Para ver la imagen proyectada, que será en la cara opuesta a aquella en que se sitúa el orificio, se substituirá la idea de “pared” por un cristal sobre el que se pueda sujetar papel tipo vegetal. Como en toda cámara oscura, las condiciones de uso siguen siendo las mismas: donde esté la imagen original hará falta luz y donde esté la cámara oscura será necesaria la mayor oscuridad posible, para poder ver con mayor definición la imagen sobre el papel.
También se ha de puntualizar que entre la primera y la tercera parte puede transcurrir un lapso de tiempo en que la actividad quede interrumpida hasta disponer de los aparatos. Así, esta actividad, dentro del aula de matemáticas se puede trabajar tanto de forma continua como de forma discontinua. Si no se quiere partir la actividad, durante el proceso de montaje de las cámaras oscuras se pueden ir trabajando los aspectos teóricos matemáticos para luego hacer las comprobaciones pertinentes en la práctica. Por tanto, la idea es que al final los cálculos y todo aquello que se pueda llevar a cabo en el marco teórico pueda tener una mínima comprobación empírica.
Para plantear los ejercicios, y más si se hace sin interrumpir el proyecto en el aula, es muy importante que se conozcan las magnitudes de las cajas oscuras que se van a construir en la realidad. De este modo los enunciados se podrán ajustar a esas medidas y así será factible una comprobación real mediante su uso, que es uno de los puntos fuertes de la actividad.
En relación al uso de lentes, cabrá ver la posibilidad de disponer de ellas, y solo se usarían, sobre todo en relación a los cálculos teóricos, para dar apoyo y ampliación al alumnado ya haya alcanzado un nivel de competencias sobresaliente en las prácticas anteriores. La dificultad aquí radicará, como he dicho, aparte de la base teórica necesaria para el alumnado, en conseguir lentes de buena calidad. Este uso de lentes también quedaría justificado para el caso de que se quiera realizar una actividad semejante en Bachillerato.
Como ya se ha indicado, se trabajará sin lentes. Esto permitirá resolver problemas que se pueden reducir al teorema de Pitágoras, Tales o a planteamientos trigonométricos sencillos.
Se presentan dos ejemplos de problema en el marco teórico, que como se verá, puede abarcar niveles de conocimientos y ejecución muy diversos.
Ejemplos de práctica
Tenemos una figura de 2 metros de altura que proyectamos dentro de la cámara oscura (Fig.2). Para cada uno de los casos planteados podemos preguntarnos, ¿Qué altura tendrá la imagen proyectada? Previo a resolver el problema, se puede pedir al alumnado que realicen una representación a escala lo más exacta posible para aproximar un primer resultado.
Fig. 2. Dos situaciones
Organización de la clase
De Gardner (2000) se deduce que el rígido agrupamiento en grupos homogéneos de alumnado no facilita el desarrollo de todos los estudiantes, y particularmente podemos colegir esta deducción en el ámbito matemático. Esto hace que se aconseje plantear agrupaciones flexibles que dependerán de las actividades a realizar. El profesorado deberá estar atento por un lado, para diseñar actividades que puedan realizar todos los miembros de cada agrupación, y por el otro, garantizar el traspaso de información tanto dentro del grupo como entre grupos.
Dentro del grupo se asignarán roles para cada parte de la actividad: representación gráfica, parte teórica y parte práctica final… sin que esto signifique que estos roles sean en absoluto excluyentes. Entre grupos se propiciarán cambios de información ya sea haciendo mezclas de alumnado puntuales, como a través de exposición de resultados. Es muy importante que a la hora de exponer los resultados todos los miembros del grupo participen de forma activa.
En el intercambio de información entre grupos se llevará término una coevaluación en que el alumnado observará y valorará a los demás, con pautas objetivas proporcionadas por el profesorado.
El papel del profesorado, pues, será de preparación teórica, de las actividades, y de dinamizador y organizador de los grupos de acuerdo con las tareas que se tengan que desarrollar en cada sesión. Fruto de la observación podrá comprobar si se alcanzan los objetivos y las competencias en cada actividad y realizar una evaluación tanto individual como a través de lo manifestado por el alumnado.
Desarrollo de las sesiones
Este ejercicio propuesto debería desarrollarse en 2 o 3 sesiones. Como veremos a continuación, habrá un guion y algunas de las partes tendrán que desarrollarse en exteriores garantizando la oscuridad (se puede conseguir con cortinas totalmente opacas) en la cámara, para así poder ver lo que se proyecta en la pantalla.
- ¿La representación es exacta? Comprobad los grados de los ángulos y las longitudes ¿Podríais hacer una representación a escala lo más exacta posible para conseguir una primera estimación de la respuesta?
- ¿Qué diferencias y similitudes significativas existen entre la primera y la segunda situación de la figura 2? A la hora de manejar una cámara oscura, ¿qué situación de las dos creéis que se dará con mayor frecuencia? ¿Por qué?
- ¿Qué herramientas matemáticas mínimas son necesarias para resolver la primera situación? Resolvedla.
- ¿Qué herramientas matemáticas mínimas son necesarias para resolver la segunda situación? Resolvedla.
- De caras a la verificación práctica, que llevaremos a cabo solo para la segunda situación, a qué distancia del suelo tiene que estar la caja oscura, o más concretamente, su orificio?
- Comparad los resultados obtenidos en los apartados 1, 4 y 5.
- Preparad una memoria escrita de la práctica y una exposición oral para explicar al resto de grupos los planteamientos hechos, procedimientos realizados y resultados obtenidos.
- Haced una evaluación del funcionamiento del grupo, destacando sus aspectos positivos así como las mejoras que proponéis.
- Haced una evaluación de los planteamientos hechos por los demás grupos, sus procedimientos y resultados, así como de su exposición (para esta parte se puede proporcionar una rúbrica al alumnado).
Atención a la diversidad en el aula
El primer recurso que ya se ha comentado anteriormente es el trabajo en grupos flexibles, que deben ir variando desde los más homogéneos a los más heterogéneos. Cuando los grupos sean homogéneos las actividades para cada uno tendrán que responder a la lógica de la agrupación. En cambio, cuando los grupos sean heterogéneos, las actividades pueden ser comunes.
Es evidente que la variedad de problemas que se pueden poner en relación a la cámara oscura es muy elevada y también es evidente que se trata de actividades que se pueden ir adaptando a las necesidades y el nivel de logro competencial del alumnado, puesto que nos podemos mover desde la simple representación gráfica de situaciones de la realidad (partiendo de una imagen distorsionada adrede por el profesorado) hasta teoremas del seno y coseno.
Se pueden plantear ejemplos en que se calculen distancias entre la caja oscura y el objeto, la altura real de una persona, objeto, árbol, edificio, etcétera.
Esta constatación permite realizar actividades dentro del marco de una escuela inclusiva, de obligada observación por vía del Decreto de la Generalitat de Cataluña 157/2017, de 17 de octubre, de la atención educativa al alumnado en el marco de un sistema educativo inclusivo. Los tipos de ejercicio que se pueden plantear en relación a la propuesta de este artículo pueden incluir sin problema medidas y soportes universales aplicables a todo el alumnado.
La combinación entre teoría y práctica se puede constatar en este tipo de ejercicio, con el que el alumnado puede primero partir de una aproximación visual, pasando por la estrictamente teórica hasta la comprobación final in situ. El factible encaje, soporte individualizado, así como la oportunidad de participación de todo el alumnado en estas actividades justifica la inclusión mencionada.
Segundo ejemplo de práctica
Este ejercicio se puede considerar de ampliación, puesto que estableceremos una relación entre geometría y funciones, como se verá. De hecho, ahonda aún más en la competencia que queremos desarrollar en esta actividad del uso del razonamiento matemático en entornos no matemáticos.
En este caso se trata de averiguar la altura de un objeto. Para ello es necesario que la imagen se ajuste perfectamente a la pantalla de la cámara oscura, como se muestra en la figura 3. Empezaremos por calcular la altura de los miembros del grupo.
Fig. 3. Altura de objeto
Desarrollo de las sesiones
Para el desarrollo de este ejercicio solo se destacarán los aspectos que sean novedosos en relación al anterior, para evitar repeticiones innecesarias.
Esta actividad debería desarrollarse también en 2 o 3 sesiones. La primera de las cuales ya necesitará una práctica con la cámara oscura, porque se partirá del cálculo de la altura de los miembros del grupo, que podrán comprobar midiéndose a sí mismos.
En este caso, pese a que el profesorado entregará otra vez un guion/cuestionario, será más importante su papel de guía, puesto que no todas las deducciones a las que se llegarán serán siempre evidentes.
- En primer lugar tenéis que medir la altura real de los miembros del grupo.
- Ahora vamos a hacer la prueba de hacer que la imagen de uno de los miembros del grupo ocupe toda la altura de la pantalla de la cámara oscura. Este punto hay que realizarlo para todos los componentes del grupo.
- ¿A qué altura está el orificio de la cámara oscura?
- ¿A qué distancia está el orificio de la cámara oscura del miembro del grupo proyectado?
- ¿Se observa alguna relación, ni que sea aproximada, entre la altura del orificio de la cámara oscura y la altura de la persona medida?
- Haced los esquemas a escala necesarios para representar todas las situaciones del apartado anterior.
- Haced los cálculos para deducir la altura de cada miembro del grupo y después deducid alguna fórmula que os dé dicha altura en función de la distancia entre la persona y el orificio de la cámara oscura.
- ¿Creéis que siempre es posible que se proyecte la imagen de un objeto de tal manera que ocupe toda la pantalla de la cámara oscura? ¿Bajo qué condiciones se puede dar? ¿Es por tanto, la cámara oscura, un objeto útil para calcular alturas de objetos mediante el método de ocupar toda la pantalla?
- Preparad una memoria escrita de la práctica y una exposición oral para explicar al resto de grupos los planteamientos hechos, procedimientos realizados y resultados obtenidos.
- Haced una evaluación del funcionamiento del grupo, destacando sus aspectos positivos así como las mejoras que proponéis.
Fijémonos que en este ejercicio se llegarán a usar los razonamientos matemáticos para, por un lado, establecer relaciones funcionales, y por el otro deducir y plantear algunas limitaciones de uso de una cámara oscura. Así, en un entorno no matemático, nuestra ciencia nos permitirá decidir alguna ocasión en la que no merece la pena, por falta de utilidad, usar el objeto construido.
En este artículo se ha pretendido por una parte dar a conocer una herramienta para el aula de matemáticas, y por el otro, dar un enfoque a la competencia de razonamiento matemático en entornos no matemáticos, todo ello enmarcado en la idea de una escuela inclusiva.
Las grandes fortalezas de este proyecto son la conexión con otras materias, la realización de un objeto y la comprobación empírica de los resultados obtenidos en los ejercicios teóricos. También entre los puntos a destacar, es relevante, como se ha visto, la relativa facilidad de poder diseñar actividades en que todos los miembros de grupos heterogéneos puedan llevar a cabo tareas y conseguir el logro de la competencia mencionada en el párrafo anterior.
También se pueden y deben realizar trabajos con grupos homogéneos, pero en este caso las actividades a desarrollar tendrán que estar bien definidas para cada uno de ellos, para evitar que se trate de una mera segregación del alumnado.
Así, pues, será tarea del profesorado, si quiere realizar prácticas con la cámara oscura, diversificar las actividades tanto para trabajar dentro del mismo grupo como para trabajar en grupos diferentes, permitiendo siempre interacciones que permitan traspasos de información en todas las direcciones.
Te puede interesar…
Amplia tu formación
¿Quieres ampliar tu formación y además conseguir puntos extra para tu baremo de méritos?
¡Consulta el completo catálogo de cursos de Campuseducacion.com!
Válidos en todas las Comunidades Autónomas y homologados por la Universidad Camilo José Cela.
¡Consigue con los cursos homologados de Campuseducacion.com 2 PUNTOS EXTRA en el baremo de méritos para las Oposiciones!
Publica con nosotros
Campus Educación Revista Digital Docente ofrece la posibilidad a la comunidad docente de publicar artículos científicos y didácticos de forma totalmente gratuita, poniendo así la divulgación del quehacer profesional docente, contribuyendo al avance de las ciencias de la información.
Los autores de Campus Educación Revista Digital Docente ven este medio un lugar ideal para la investigación pedagógica, a la vez que reciben un certificado de autoría que les puede ayudar a sumar puntos en diferentes procesos selectivos y baremos de méritos, como las oposiciones docentes o el concurso general de traslados.
Ahora puedes conseguir 4 certificaciones en Campus Educación Revista Digital Docente si te matriculas en tres o más cursos homologados para oposiciones o concurso general de traslados en Campuseducacion.com